The Big Here 02: What Time is Sunset Today?

This continues a series of ruminations, discussion on method, and answers to Kevin Kelly’s The Big Here, a query and challenge to know the space we live in, in its shape and relationships.

2) What time is sunset today?

One of the pleasures of living in the north half of the Northwest is the difference in the length of the days, from season to season. Not like Alaska, of course, but they might be taking things a little too far up there. Here, at least, the sun comes up every day. Still, a lot of people have trouble with those winter days when you go to work in the dark and come home after sunset. I’ll take that because it gives us these nights in midsummer when it’s still light enough to move around at 10:00.

I tend to notice the sunrise and set times throughout the year, though for reasons that vary with the seasons. During the late fall and early spring, I notice the change because it’s a qualitatively different experience to talk to and from work in the dark, as opposed to during the daylight. I spend as much time in the woods as I can, especially, but not exclusively during the late spring, summer, and early fall, and the amount of daylight matters for what I’m able to do. Because of this, I know that the latest sunset for Olympia is around 9:10, at midsummer. I also know that the sun sets at about 7:10 at the equinox (and we have just over twelve hours of daylight – “equi” indeed).

Until I started looking at this closer in preparation for writing this, I thought I could estimate the sunset for tonight using a simple proportion between those two times, which results in 8:25. The real answer is 8:53, because the change is not linear, but a curve. In the three months between the solstice and the equinox in September, the sunset changes about two hours, with 20 minutes in first month, 40 minutes in the next, and 60 minutes during the last. So, a new method would be to use the new proportions and say that we’re a little past that first month, which gives an estimate of about 8:50. Closer.

I learned this from the data that I pulled from the U.S. Naval Observatory’s Data Services site. And I built this chart from it. (Click on the image for a full size view.)


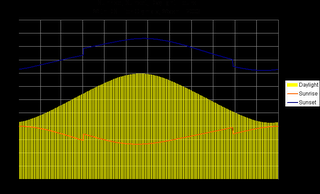
So, my new method for estimating sunset, at least for summer, is to determine how many months from the spring equinox we are and assign 20 minutes for the first (one-sixth of the 120 minutes change), 40 for the second (one-third of 120), and 60 for the third (or one-half of the total). I can use the same proportions for partial months. So, August 1 is about ten days into the second month, so it gets one-sixth of the second month’s 40 minutes, or 7 minutes. Subtracting 27 minutes from 9:11 results in 8:44, which is right on.